A history of computing I: The Antikythera Mechanism

A very special corroded lump of bronze

This is the first article in the series about the history of computing. Here, we look at the remarkable Antikythera Mechanism - a piece of extraordinary complexity for the period.

A timeline

Spring 1900 – the wreck of an ancient Roman ship filled with archaeological treasures is found off the coast of Antikythera in Greece by Captain Dimitrios Kontos

1900-1901 – recovery of artefacts from the shipwreck.  Amongst them are statues, coins, jewellery, pottery and a corroded wooden box containing a corroded lump of bronze.

May 1902 – archaeologist Valerios Stais noticed what was apparently a gear wheel within the structure. His fellow archaeologists considered that his theory – that the mechanism was a type of astronomical calculator – could not have been built back in that era.

1951 - science historian Derek J. de Solla Price became interested in the artefact. In 1971, he started working with physicist Charalampos Karakalos scanning the extant parts of the device with X-rays and Gamma rays to create the first 3-D image of the interior. It turns out that the archaeologist Stais was correct.

The Antikythera mechanism is now regarded as the earliest known example of an analogue computer.

Capabilities

The Antikythera mechanism could calculate (at least) the following:

• The paths of the visible planets – Mercury, Venus, Mars, Jupiter and Saturn,
• The paths of the Sun and Moon, and the phases of the moon,
• Solar and Lunar eclipses,
• The four-year cycle of the Ancient Greek games.

The implication is that this sophisticated machine must have been pre-dated by other, equally complex, devices, but sadly lost in the mists of time.

The Greek astronomers and mathematicians took lessons from their Babylonian and Egyptian predecessors, all of whom were working with an extra level of complexity.

Their understanding of the cosmos was geocentric, that is, they believed that the Earth was the centre of the universe, and this led to calculations that were both epicyclic – wheels within wheels – and eccentric – offset – calculations.

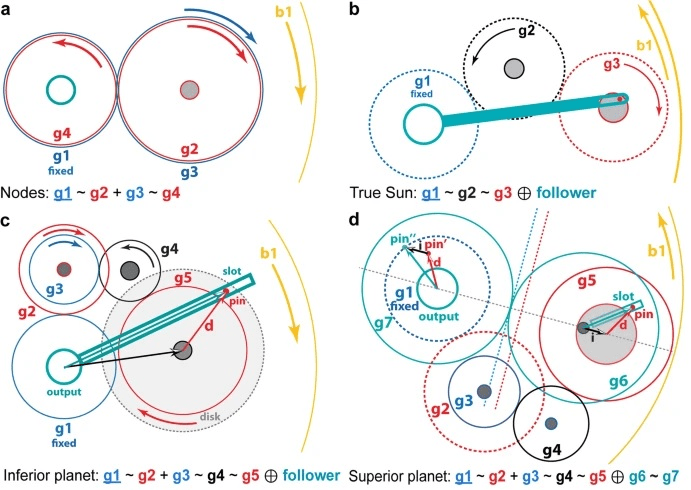
Gear models of the mechanism

They managed to create a model based on retrograde motion – the apparent reversal of a planet’s movement against the starry backdrop.  They then created ratios to calculate where a planet would be.  These ratios are expressed as two numbers. So for Venus, the most accurate ratio was 720, 1511, which means that it should show retrograde motion 720 times in 1511 years.

Normally this would involve impossibilities (for the time) of creating cogwheels that correspond to very high (and sometimes prime) numbers – for example, for the planet Venus, you would require a cog with 1,151 teeth for more accurate predictions.

However, as recently as 2016, researchers found an inscription of the number 462 on the front cover in the Venus section and 442 in the Saturn section.

This was a major breakthrough.

Recreation of the rear panel

With the new figures plugged into the calculations, we arrive at a cycle of (289, 462) for Venus and (447, 442) for Saturn. These numbers are highly accurate for predicting planetary motion, but they are factorisable.

This means that they are divisible by other numbers, unlike prime numbers. This in turns allows for the construction of the device with cogs of less than one hundred teeth, keeping it compact and easier to build.

Unfortunately, the inscriptions for the other planets have not been readable.

Three aims

The designer of this box had three aims in mind when creating it:

• accuracy – make it as accurate as possible,
• factorisibility – one example in the mechanism is one of the gears has seventeen teeth – and
• economy – the seventeen-teeth gear is used for different planetary motions.

Now that the mathematics had been worked out, it was then time for a group of artisans to create the physical mechanism itself.

From the most recent scans, it was an exquisitely built machine, calculating the motion of the planets, the Sun, the Moon (and its phases) and also had a “Dragon Hand” that predicted eclipses on the front.

Recreation of the front panel

Both front and rear panels were finely inlaid and detailed, and there is some speculation that the mechanism was covered in precious stones. The whole thing was powered by a hand crank on the side.

Articles by the same author:

Comparaison de différents logiciels de dépôt

Dépôt de logiciels et gestion des versions

Sources:

https://www.nature.com/articles/s41598-021-84310-w

Further viewing:

https://www.nature.com/articles/s41598-021-84310-w#MOESM4

Images:

Zde, CC BY-SA 4.0, via Wikimedia Commons ; marsupium photography, CC BY-SA 2.0, via Wikimedia Commons ; Gts-tg, CC BY-SA 4.0, via Wikimedia Commons